Region between Polar Curves

14 July 2014

Every once in a while you’ll get a piece of maths which will elicit a response of “wat?”

Find the area of the region inside the rose r=4sin⁡2θr=4\sin2\theta and inside the circle r=2r=2.

Being derived from the area of a sector, it follows that the area between two polar curves on the interval aa to bb should be

A=12∫ab([f(θ)]2−[g(θ)]2) dθ.A = \frac{1}{2}\int_{a}^{b}\left( \left[f(\theta)\right]^2 - \left[g(\theta)\right]^2 \right)\,d\theta.

The usual disclaimers apply: f(θ)f(\theta) should be greater than g(θ)g(\theta) for θ∈[a,b]\theta\in\left[a,b\right]; f(θ)f(\theta) and g(θ)g(\theta) should be integrable on [a,b]\left[a,b\right].

Even the graph seems to support this idea, at first glance.

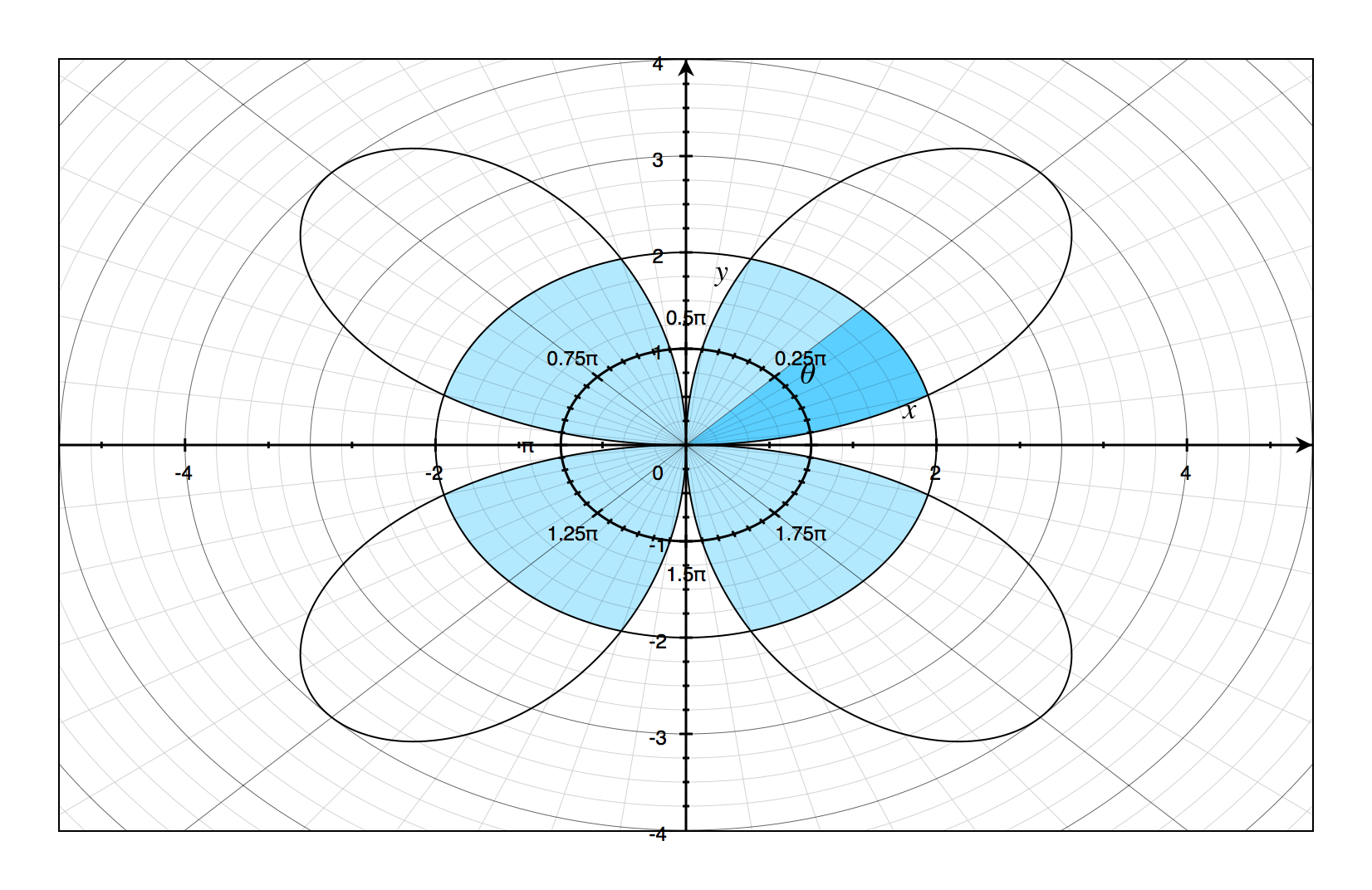
polargraph

Using some symmetry arguments (area of half a petal, multiplied by eight to equal four whole petals), you might think that the area of the region is

A≠8⋅12∫0π4[(4sin⁡2θ)2−22]dθ.A\neq8\cdot\frac{1}{2}\int_{0}^{\frac{\pi}{4}}\left[(4\sin2\theta)^2-2^2\right]d\theta.

If you try and evaluate that integral, you’ll find it equal to 4π4\pi, only that is not the area of the shaded region.

wat

The area of the shaded region is actually computed using two different integrals, which should become more apparent when the graph is re-plotted on the Cartesian plane.

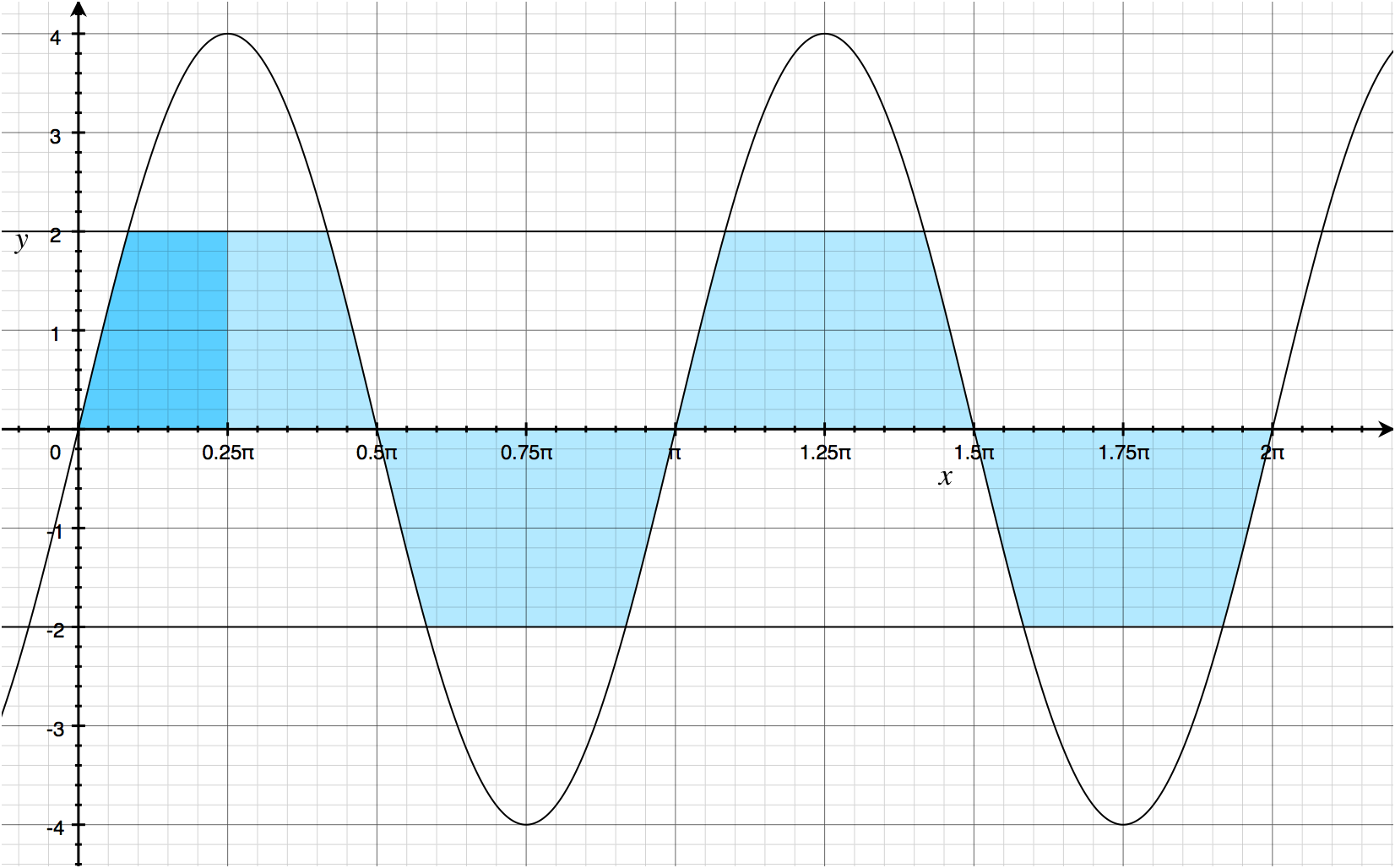
cartgraph

For the first little region, the area is dependent upon only r=4sin⁡2θr=4\sin2\theta, and for the rest of the region the area depends only on r=2r=2. Knowing exactly where those regions lie on the independent (θ\theta) axis is, pardon the pun, integral to correct solution.

Finding the point is actually quite trivial: set the two equations equal to each other and solve.

2=4sin⁡2θ12=sin⁡2θ2θ=arcsin⁡12θ=12arcsin⁡(12)\begin{array}{rcl} 2&=&4\sin2\theta\\ \frac{1}{2}&=&\sin2\theta\\ 2\theta&=&\arcsin\frac{1}{2}\\ \theta&=&\frac{1}{2}\arcsin\left(\frac{1}{2}\right) \end{array}

Therefore, sin⁡2θ=12\sin2\theta=\frac{1}{2} when θ∈{π12+nπ,5π12+nπ} ,n∈Z\theta\in\left\{\frac{\pi}{12}+n\pi,\frac{5\pi}{12}+n\pi\right\}\,,n\in\mathbb{Z}.

Using this information, our pair of integrals becomes

A=8⋅12[∫0π1216sin⁡22θ dθ+∫π12π44 dθ].A=8\cdot\frac{1}{2}\left[\int_{0}^{\frac{\pi}{12}}16\sin^2 2\theta\,d\theta+\int_{\frac{\pi}{12}}^{\frac{\pi}{4}}4\,d\theta\right].

From this we can correctly conclude that A=43(4π−33).A = \frac{4}{3}\left(4\pi-3\sqrt{3}\right).

Wat indeed.